이번에는 백준 24060번 문제를 통해 병합 정렬 개념을 다시 다져보자.
이번 문제도 저번 개념 정리와 같이 재귀 방식으로 계속 나누고
병합하며 정렬한다.
[ 알고리즘 ] 병합 정렬 - JAVA
백준 24060번 문제를 풀기 전에 병합 정렬 알고리즘의 로직에 대해아주 자세히 포스팅 해보려 한다. 사실 이미지로 본다면 아주 쉬운데 이걸 구현하고자 하면 머리가 아플 수도 있다. 때문에 이
p-coding.tistory.com


🔍 문제 핵심
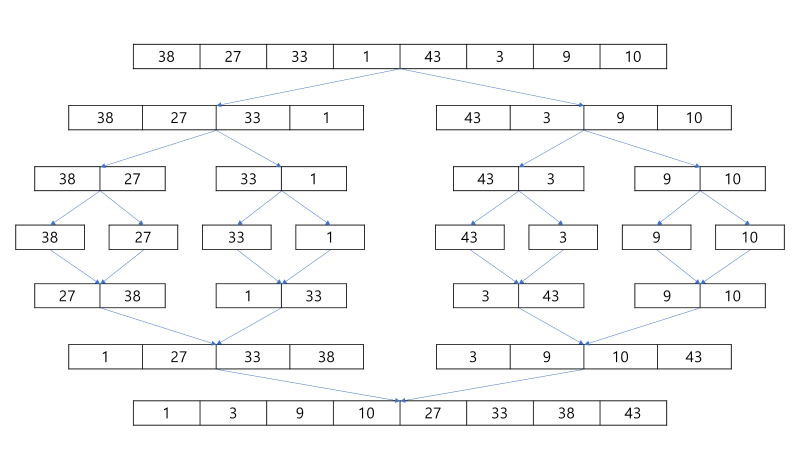
- 병합 정렬은 정렬 알고리즘 중 하나로, 분할 정복(Divide and Conquer) 방법을 사용한다.
- 주어진 배열을 계속해서 절반으로 나누고, 더 이상 나눌 수 없을 때까지 나눈 뒤, 정렬된 상태로 병합한다.
- 문제에서 예시로 주어진 병합 정렬 과정을 잘 이해하고, 이를 직접 구현해보는 것이 핵심이다.
📌 병합 정렬이란?
1. 분할 (Divide)
- 배열을 절반으로 나눈다.
- 이 과정을 배열의 크기가 1이 될 때까지 반복한다.
- 각 하위 배열은 재귀적으로 처리된다.
2. 정복 (Conquer)
- 크기가 1인 배열끼리 **두 개씩 병합(Merge)**하며 정렬해나간다.
- 병합 과정에서 두 배열의 원소를 비교하여 작은 값을 먼저 넣는 방식으로 정렬이 이루어진다.
3. 병합 (Combine)
- 정렬된 두 배열을 하나로 합치며 정렬을 유지한다.

재귀 방식으로 정렬하는 복잡한 구조로 공부하기 좋은 문제이다.
이해도를 높이기 위해 많은 관련 문제를 푸는 것을 추천한다.
전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static int count = 0;
private static int number = -1;
private static int K;
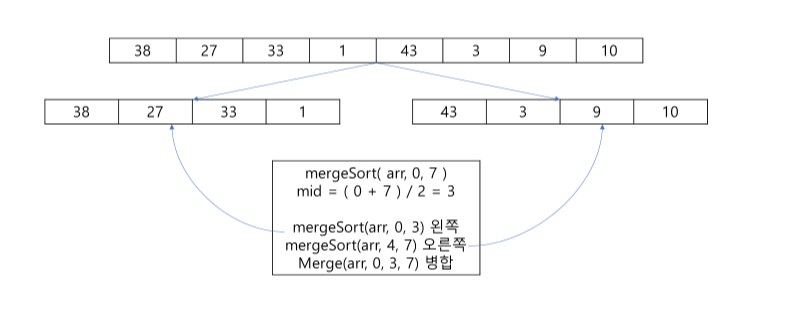
private static void mergeSort(int[] arr, int left, int right) {
if(left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
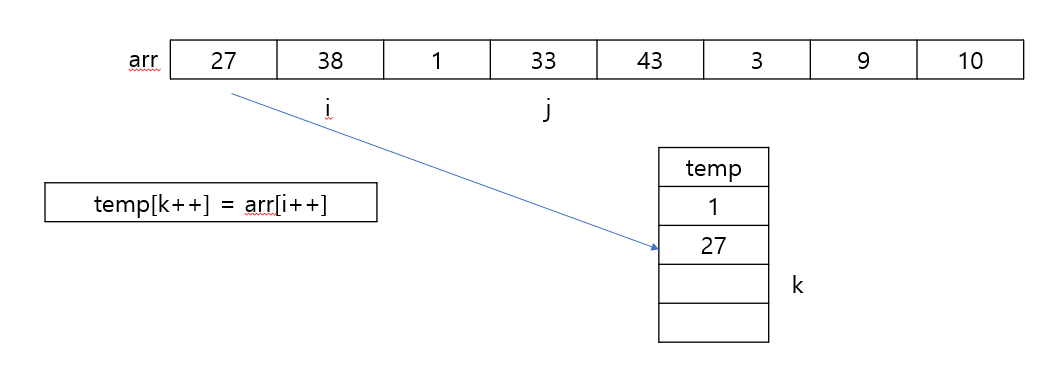
private static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int i = left, j = mid + 1;
int z = 0;
while(i <= mid && j <= right) {
if(arr[i] <= arr[j]) {
temp[z++] = arr[i++];
}
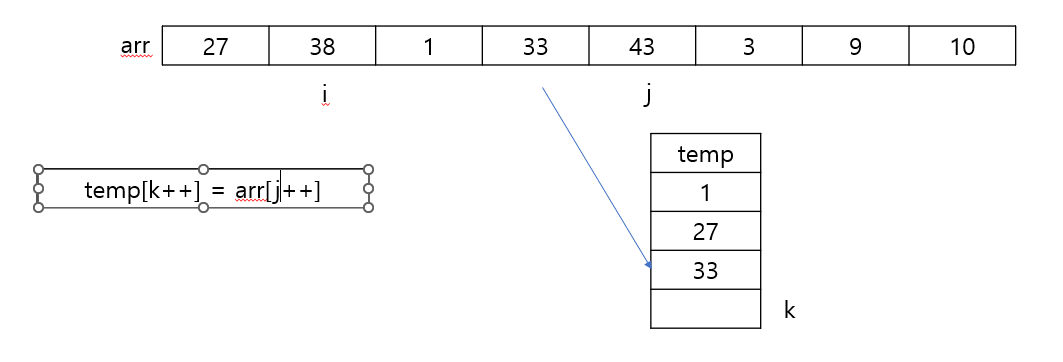
else {
temp[z++] = arr[j++];
}
}
while(i <= mid) {
temp[z++] = arr[i++];
}
while(j <= right) {
temp[z++] = arr[j++];
}
for (int l = 0; l < temp.length; l++) {
arr[left + l] = temp[l];
count++;
if(count == K) {
number = temp[l];
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
int N = Integer.parseInt(stringTokenizer.nextToken());
K = Integer.parseInt(stringTokenizer.nextToken());
int[] arr = new int[N];
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(stringTokenizer.nextToken());
}
mergeSort(arr, 0, N - 1);
System.out.println(number);
}
}'백준 단계별 풀이' 카테고리의 다른 글
| [ 백준 15651번 문제 ] N과 M (3) - JAVA (1) | 2025.05.24 |
|---|---|
| [ 백준 15650번 문제 ] N과 M (2) - JAVA (1) | 2025.05.23 |
| [ 백준 4779번 문제 ] 칸토어 집합 - JAVA (0) | 2025.04.03 |
| [ 백준 15649번 문제 ] N과 M (1) - JAVA (1) | 2025.03.24 |
| [ 백준 26069번 문제 ] 붙임성 좋은 총총이 - JAVA (1) | 2025.03.12 |