이번 글에서는 큐, 스택에 마무리 문제인 24511번 문제를 해결해 보자.
시간 제한과 메모리 제한이 까다로울 것으로 예상된다.
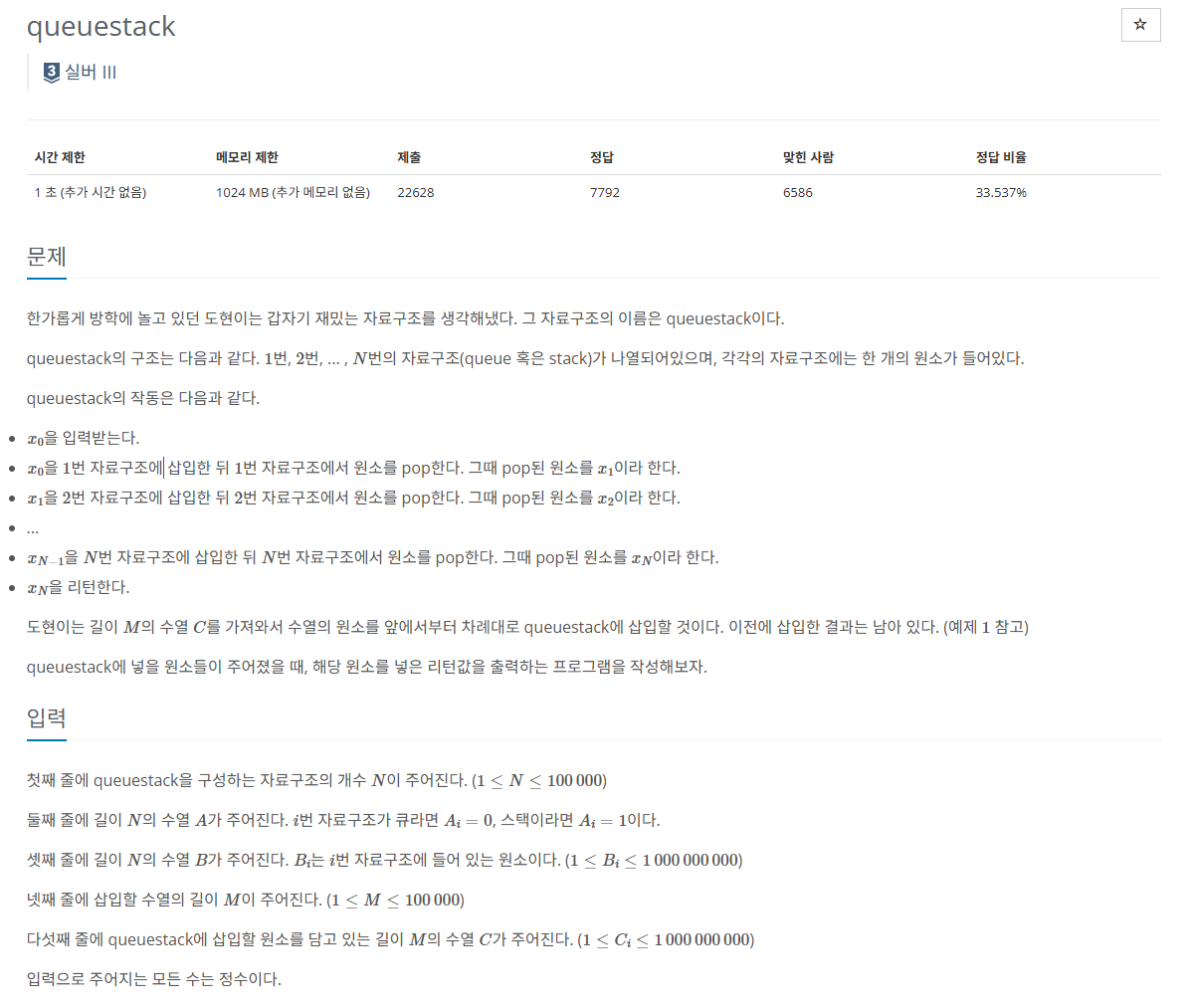
문제 핵심
- 첫째 줄 - 자료구조의 수 : N
- 둘째 줄 - 수열의 종류 : 0 ( Queue ), 1 ( Stack )
- 셋째 줄 - 자료구조의 초기값 설정
- 넷째 줄 - 삽입할 수열의 길이 : M
- 다섯째 줄 - 삽입할 수열의 원소들
풀이 과정
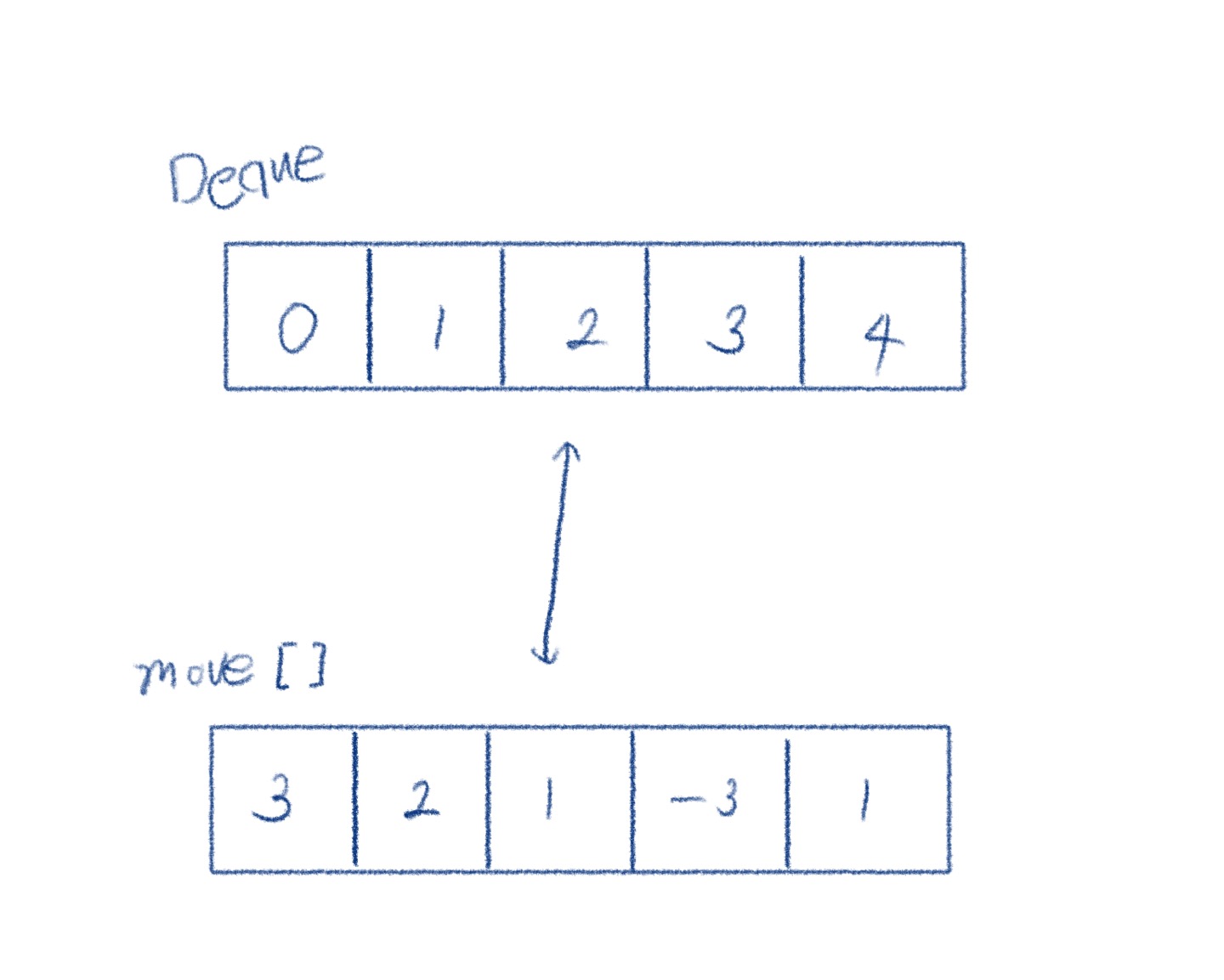
첫 번째 예제의 과정 중 첫 번째 스텝을 다음과 같이 나타낼 수 있다.
그림 처럼 queue와 stack을 구현하여 값을 삽입하고 제거하는 과정으로 구현해보자.
아마 메모리에서 먼저 초과되지 않을까 싶다.

1. 자료구조 저장
0, 1과 구별 값에 따라 큐인지 스택인지 구별하여 저장한다.
List<Object> dataStructure = new ArrayList<Object>();for (int i = 0; i < N; i++) {
int type = Integer.parseInt(stringTokenizer.nextToken());
if (type == 0) {
dataStructure.add(new LinkedList<Integer>());
} else {
dataStructure.add(new Stack<Integer>());
}
}
2. 초기 값 저장
세번 째 줄의 초기 값들을 저장한다.
이 때 초기값들은 instanceof를 통해 자료구조를 판별 후 맞는 메소드를 사용한다.
for (int i = 0; i < N; i++) {
int num = Integer.parseInt(stringTokenizer.nextToken());
if (dataStructure.get(i) instanceof Queue) {
((Queue<Integer>) dataStructure.get(i)).offer(num);
} else {
((Stack<Integer>) dataStructure.get(i)).add(num);
}
}
3. 메인 과정
새로운 값 들이 큐와 스택을 지나면서 반복되는 과정이다.
이 때, 사실 스택이 값을 거쳐가기만 하기 때문에 의미가 없다.
for (int i = 0; i < M; i++) {
int num = Integer.parseInt(stringTokenizer.nextToken());
int temp = num;
for (int j = 0; j < N; j++) {
if (dataStructure.get(j) instanceof Queue) {
((Queue<Integer>) dataStructure.get(j)).add(temp);
temp = ((Queue<Integer>) dataStructure.get(j)).remove();
}
}
stringBuilder.append(temp).append(" ");
}
결과는 시간 초과로 메모리 문제가 아닌 2 중 for문에 N과 M의 최악의 경우 (On2)
100,000 * 100,000 = 10,000,000,000 기 때문에 벌어진 일이다.
그렇다면 2 중 for문의 구조를 제거하고,
스택구조에서 값은 지나치기만 하기 때문에 경우에서 제거한다.
4. 자료구조의 재구성
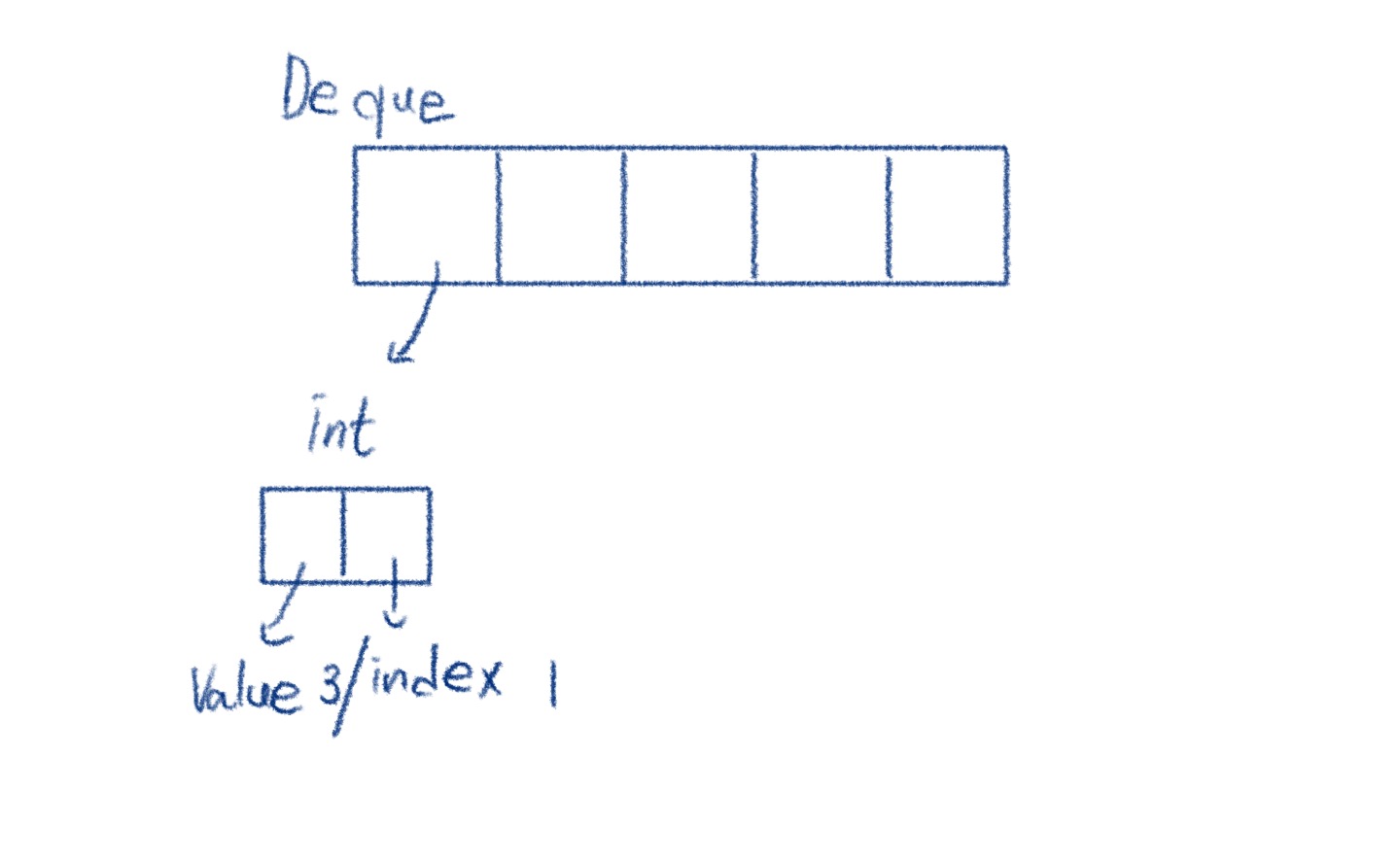
그렇다면 큐의 구조일 때 값을 교체하는 과정이고, 그게 여러개라면 하나씩 밀려나는 과정이다.
큐 여러개가 하나의 값만 가지고 있기 때문에 여러개의 큐가 하나의 큐가 되어버린다.
( 즉, 다음과 같은 구조일 때 새로운 값이 들어온다면 하나의 큐처럼 행동한다. )

그렇다면 하나의 큐를 생성하고 큐일 경우에만 값을 추가한다.
Deque<String> queue = new ArrayDeque<>();
StringBuilder stringBuilder = new StringBuilder();
int N = Integer.parseInt(bufferedReader.readLine());
String[] dataStructureString = bufferedReader.readLine().split(" ");
String[] valueString = bufferedReader.readLine().split(" ");
for (int i = 0; i < N; i++) {
int type = Integer.parseInt(dataStructureString[i]);
if(type == 0){
queue.addLast(valueString[i]);
}
}
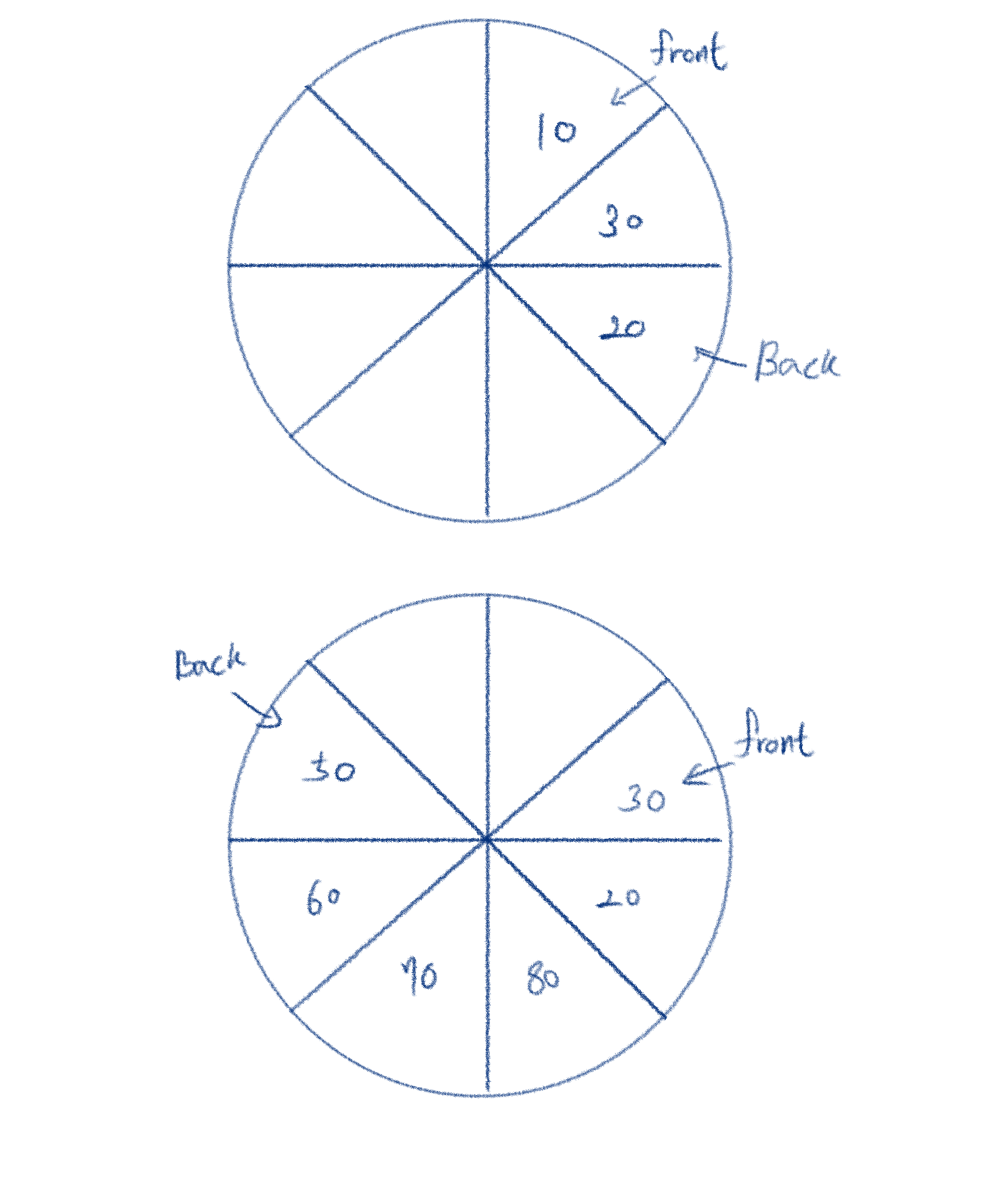
5. 메인 과정 재구성
다음과 같이 큐의 삽입과 삭제를 반복하면 O(n)의 경우의 수와 메모리 문제가 모두 해결된다.
int M = Integer.parseInt(bufferedReader.readLine());
String[] addValueString = bufferedReader.readLine().split(" ");
for (int i = 0; i < M; i++) {
queue.addFirst(addValueString[i]);
stringBuilder.append(queue.removeLast()).append(" ");
}

이번 문제는 마치 알고리즘이 큐처럼 행동하게 하여 해결할 수 있었다.
다음과 같이 자료구조의 개념을 이해한다면 여러방법으로 구현할 수 있다.
줄 서거나(큐), 박스에 물건을 넣고 빼거나(스택) 처럼 한 가지로 제한되지 않는다는 점이다.
시간과 메모리를 줄여야 한다는 점에서 이런 구조를 생각할 수 있었던 문제였다.
실패 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
List<Object> dataStructure = new ArrayList<Object>();
StringTokenizer stringTokenizer;
StringBuilder stringBuilder = new StringBuilder();
int N = Integer.parseInt(bufferedReader.readLine());
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < N; i++) {
int type = Integer.parseInt(stringTokenizer.nextToken());
if (type == 0) {
dataStructure.add(new LinkedList<Integer>());
} else {
dataStructure.add(new Stack<Integer>());
}
}
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < N; i++) {
int num = Integer.parseInt(stringTokenizer.nextToken());
if (dataStructure.get(i) instanceof Queue) {
((Queue<Integer>) dataStructure.get(i)).offer(num);
} else {
((Stack<Integer>) dataStructure.get(i)).add(num);
}
}
int M = Integer.parseInt(bufferedReader.readLine());
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int i = 0; i < M; i++) {
int num = Integer.parseInt(stringTokenizer.nextToken());
int temp = num;
for (int j = 0; j < N; j++) {
if (dataStructure.get(j) instanceof Queue) {
((Queue<Integer>) dataStructure.get(j)).add(temp);
temp = ((Queue<Integer>) dataStructure.get(j)).remove();
}
}
stringBuilder.append(temp).append(" ");
}
System.out.println(stringBuilder);
}
}성공 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Deque;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
Deque<String> queue = new ArrayDeque<>();
StringBuilder stringBuilder = new StringBuilder();
int N = Integer.parseInt(bufferedReader.readLine());
String[] dataStructureString = bufferedReader.readLine().split(" ");
String[] valueString = bufferedReader.readLine().split(" ");
for (int i = 0; i < N; i++) {
int type = Integer.parseInt(dataStructureString[i]);
if(type == 0){
queue.addLast(valueString[i]);
}
}
int M = Integer.parseInt(bufferedReader.readLine());
String[] addValueString = bufferedReader.readLine().split(" ");
for (int i = 0; i < M; i++) {
queue.addFirst(addValueString[i]);
stringBuilder.append(queue.removeLast()).append(" ");
}
System.out.println(stringBuilder);
}
}'백준 단계별 풀이' 카테고리의 다른 글
| [ 백준 1010번 문제 ] 다리 놓기 - JAVA (2) | 2025.03.08 |
|---|---|
| [ 백준 11050번 문제 ] 이항 계수 1 - JAVA (2) | 2025.03.05 |
| [ 백준 2346번 문제 ] 풍선 터뜨리기 - JAVA (2) | 2025.03.02 |
| [ 백준 28279번 문제 ] 덱 2 - JAVA (1) | 2025.03.01 |
| [ 백준 11866번 문제 ] 요세푸스 문제 0 (2) | 2025.03.01 |